Finite difference Method for 1D Laplace Equation

Home > Numerical Analysis > Finite difference Method for 1D Laplace Equation

Finite difference Method for 1D Laplace Equation

October 18, 2012 beni22sof Leave a comment Go to comments

I will present here how to solve the Laplace equation using finite differences. First let’s look at the one dimensional case:

$\displaystyle \begin{cases} -u''=1 & \text{ in }[0,1] \\ u(0)=u(1)=0. \end{cases}$

In this case it is easy to solve explicitly the differential equation and get that $u(x)=\frac{1-x^2}{2}$ . However, sometimes it is not so easy or not possible at all to find an explicit solution, and there are some numerical methods which can be used to approximate our solution. In the one dimensional case, or in the case of a rectangular domain or a box in superior dimensions, the method of finite differences can be sucessfully used.

Pick a step ${h=1/N}$ , where ${N}$ is a positive integer. Then we use the approximations ${u'(x)\simeq \displaystyle \frac{u(x+h)-u(x)}{h}}$ and $u''(x) \simeq \frac{u(x+h)+u(x-h)-2u(x)}{h^2}$ .

We replace our function ${u}$ by a discretization ${u_k=u(k/N)}$ and the derivative ${u''}$ becomes ${-2u_i+u_{i+1}+u_{i-1}}$ . The boundary conditions translate to ${u_0=u_N=0}$ . Now on the points situated in the interior of ${(0,1)}$ we have the relations:

$\displaystyle \frac{1}{h^2}(2u_i-u_{i+1}-u_{i-1})=1,\ i=1..N-1,$

and these translate to a system of equations

$\displaystyle Au=f$

where ${A}$ is an ${N-1 \times N-1}$ matrix

$\displaystyle A=\frac{1}{h^2}\begin{pmatrix} 2 & -1 & 0 &\cdots & 0 \\ -1 & 2 & -1 & \cdots & 0 \\ 0& -1 & 2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 2 \end{pmatrix}=\frac{1}{h^2}\text{tridiag}(-1,2,-1)$

and ${f}$ is a column vector of length ${N-1}$ of ones. Since ${A}$ is invertible (a recurrence relation can be found for ${\det(A)}$ ) the presented system has a unique solution, which will be the desired approximation by finite differences of our function.

We can change the boundary conditions to ${u(0)=a}$ and ${u(1)=b}$ by changing ${f_1}$ and ${f_{N-1}}$ using the formulas

$\displaystyle f_1=1+N^2a,\ f_{N-1}=1+N^2 b.$

In a similar way we can solve numerically the equation

$\displaystyle \begin{cases} -u''=f & \text{ in }[0,1] \\ u(0)=u(1)=0. \end{cases}$

where ${f}$ is, for example, an arbitrary continuous function.

Below I present a simple Matlab code which solves the initial problem using the finite difference method and a few results obtained with the code.

function u = laplacefd1(n); x=linspace(0,1,n+1); A=sparse(diag(2*ones(n-1,1))+diag((-1)*ones(n-2,1),1)+diag((-1)*ones(n-2,1),-1)); left=0; right=0; f=ones(n-1,1); f(1)=f(1)+(n)^2*left; f(n-1)=f(n-1)+(n)^2*right; u=(n)^2*A\f;

Different boundary conditions

Dirchlet boundary conditions

Categories: Numerical Analysis Tags: finite difference, MATLAB, numerical analysis

Comments (6) Trackbacks (0) Leave a comment Trackback

Hannie Grace Jalon

October 7, 2016 at 11:24 pm

Reply

where do these formulas: \displaystyle f_1=1+N^2a,\ f_{N-1}=1+N^2 b come from??
is this based from solving \displaystyle \frac{1}{h^2}(2u_i-u_{i+1}-u_{i-1})=1, for i=1 and i=N ??
how did you get a “+N^2” in each formula?
- beni22sof
  
  October 8, 2016 at 1:07 am
  
  Reply
  
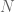  Yes, the formulas come from the discrete Laplacian formulation. Note that $h=1/N$ so $1/h^2 = N^2$ . That’s why you get an $N$ squared in the formulas.
  
  To see more precisely why it is enough to change $f_1,f_N$ just write the discrete Laplacian for $u_0,u_1,u_2$ . You’ll get $N^2(2u_1-u_0-u_2) = f_1$ . Now if you pass the term with 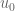$u_0$ to the other side you see that you have the same matrix equation like in the zero boundary condition, but with different $f$ .
David

February 8, 2017 at 2:28 pm

Reply

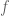Hi, in your first equation you have the problem -u”=1 with boundary conditions u(0) = u(1) = 0. You state that the analytical solution to this problem is 0.5*(1-x^2).

Now when I insert the boundary condition into your analytical solution, I get u(0) = 0.5*(1-0^2) = 0.5.

Are you sure the boundary conditions in your problem are correct?
- beni22sof
  
  February 22, 2017 at 4:51 pm
  
  Reply
  
  You are right. The solution in my post is, in fact, on the interval [-1,1]. In order for it to work on [0,1] you need to change it a bit. I guess 0.5*x*(x-1) should work instead.
poso

November 4, 2017 at 8:21 pm

Reply

here must to
loiosu

November 5, 2017 at 6:20 am

Reply

An initial