Sleek proof that the harmonic series diverges

Home > Analysis, Measure Theory > Sleek proof that the harmonic series diverges

Sleek proof that the harmonic series diverges

April 14, 2012 beni22sof Leave a comment Go to comments

Suppose that the harmonic series does converge. Then the sequence of integrable functions functions $f_n : \Bbb{R}_+ \to \Bbb{R}_+,\ f_n=\frac{1}{n} \chi_{[0,n]}$ is bounded above by an integrable function $g: \Bbb{R}_+ \to \Bbb{R}_+,\displaystyle \ g=\sum_{i=1}^\infty \frac{1}{i} \chi_{[i-1,i]}$ .

Therefore, since $f_n \to 0$ almost everywhere, the Dominated Convergence theorem applies and we have

$0=\int_0^\infty \lim_{n \to \infty}f_n = \lim_{n \to \infty}\int_0^\infty f_n=1,$

and we have reached a contradiction. Therefore the harmonic series diverges.

Source: http://mathoverflow.net/questions/42512/awfully-sophisticated-proof-for-simple-facts/44742#44742

In the following blog post there are two links in which over 40 ideas of proof are presented, all different from the one presented here.

Categories: Analysis, Measure Theory Tags: dominated convergence, harmonic, trick

Comments (7) Trackbacks (0) Leave a comment Trackback

removablesingularity

April 24, 2012 at 8:27 am

Reply

Is there a similar argument for:

$\sum_{i=1}^\infty \frac{1}{n^2}$
beni22sof

April 24, 2012 at 12:23 pm

Reply

The proof works for proving the divercence of $\sum_{i=1}^\infty \frac{1}{n^\alpha}$ for $\alpha < 1$ . I don't think that the proof can be adapted to prove the convergence of the harmonic series for $\alpha > 1$ , because it assumes the convergence in order to reach a contradiction.
Jj

November 4, 2013 at 2:21 pm

Reply

But why wouldn’t the same proof work for $\sum \frac{1}{2^n}$ ? We assume it converges, then we get a contradiction.
- beni22sof
  
  November 4, 2013 at 2:40 pm
  
  Reply
  
  I believe you want to say: $\sum \frac{1}{n^2}$ .
  
  If we define $f_n = \frac{1}{n^2} \chi_{[0,n]}$ then the integral of $f_n$ over $[0,n]$ is $1/n$ which converges to zero, so we don’t have a contradiction.
  - Jj
    
    November 4, 2013 at 6:34 pm
    
    What I meant was defining $f_n=\frac{1}{2^n}\chi_{[0,2^n]}$ , then the integral of $f_n$ is 1.
beni22sof

November 4, 2013 at 8:03 pm

Reply

Jj :

What I meant was defining $f_n=\frac{1}{2^n}\chi_{[0,2^n]}$ , then the integral of $f_n$ is 1.

Then you have $g = \sup_n f_n = \sum_{n \geq 1} \frac{1}{2^n} \chi_{(2^{n-1},2^n]}$ , and the integral of $g$ is $\sum_{n \geq 0} \displaystyle \frac{2^n -2^{n-1}}{2^n}=\sum_{n\geq 0} \frac{1}{2}\ (\star)$ which is divergent. This means that you cannot bound $f_n$ by an integrable function $g$ so Lebesgue dominated theorem does not apply.

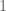Note that the difference between $\sum_{n \geq 1} \frac{1}{n}$ and $\sum_{n \geq 1}\frac{1}{2^n}$ is that the difference between consecutive terms is $1$ for the first one, and $2^n-2^{n-1}$ for the second one and that difference appears at the denominator in $(\star)$ .
- Jj
  
  November 4, 2013 at 8:12 pm
  
  Reply
  
  Thanks, I appreciate it.