Best linear interpolation constant on a triangle
Given a triangle in the plane one may ask what is the best estimate one can get for the difference between a
function
defined in
and the linear function taking the same values at the vertices of the triangle
. The difference
should be evaluated in some norm involving the derivatives of
.
When dealing with finite element estimations it is a natural question to try and bound the difference of the gradients in :
since the
estimate is usually easier to obtain. Since solutions of PDEs are often in
, i.e. the second derivatives have bounded
norms, it is natural to ask if it is possible to find a constant
such that
where is the semi-norm involving only integrals of the second derivatives of
. It turns out that such a constant exists and finding the dependence on
on the triangle
is a challenging question and an active field of research. This is mainly due to the fact that knowing explicitly the constant
immediately gives useful and explicit error bounds for solutions of finite element problem. With the rise of the research domain of validated computing, this is an essential topic.
Let me name a few papers where such results are discussed:
- Estimation of interpolation error constants for the P0 and P1 triangular finite elements by Fumio Kikuchi and Xuefeng Liu: https://doi.org/10.1016/j.cma.2006.10.029 In this paper, explicit formulas for
are given in terms of the elements of the triangle. This is quite useful if the mesh contains triangles with variable geometries.
- For a fixed triangle
, the optimal constant is in fact related to the first eigenvalue of a fourth order problem. This is discussed in the following note by Handscomb: https://www.math.auckland.ac.nz/~waldron/Multivariate/handscomb95.pdf
- Kobayashi proposes multiple explicit formulas for the constant C in https://am2015.math.cas.cz/proceedings/contributions/kobayashi.pdf The proofs are not complete, but they are verified for a large class of triangles through discrete eigenvalue problems. Indeed, using a triangulation of
with congruent triangles and finding the discrete eigenvalue on that triangulation for the minimization of the quotient
with the Morley finite elements gives an explicit upper bound for the constant.
Iterative algorithms – Convergence rates
In optimization and any other iterative numerical algorithms, we are interested in having convergence estimates for all algorithms. We are not only interested in showing that the error goes to , although that is essential, but also at what speed the error goes to
. An algorithm which converges quicker is a better choice in all cases!
Generally, there are two points of view for convergence: convergence in terms of where
is the number of iterations or having a comparison between the error at iteration
and the error at the iteration
. I will take the latter point of view below.
To fix the ideas, denote the error estimate for
, where
is the current iterate and
is the solution to the problem.
We have the following standard classification:
- linear convergence: there exists
such that
the constant
is called the convergence ratio
it is easy to show that
, so in particular
.
- sublinear convergence:
but is not linearly converging
- superlinear convergence:
with any positive convergence ratio
sufficient condition:
- {convergence of order
}: there exists
such that for
large enough
is called the order of convergence
the case
has a special name: quadratic convergence
To underline the significant difference between linear and superlinear convergence consider the following examples: Let . Then:
converges linearly to zero, but not superlinearly
converges superlinearly to zero, but not quadratically
converges to zero quadratically
Quadratic convergence is much faster than linear convergence.
Among optimization algorithm, the simpler ones are usually linearly convergent (bracketing algorithms: trisection, Golden search, Bisection algorithm, gradient descent). Algorithms involving higher order information or approximation are generally superlinear (Secant method, Newton, BFGS or LBFGS in higher dimensions etc.).
There is a huge difference between linear convergence and super-linear convergence. If a faster algorithm is available using it is surely useful!
Golden search algorithm – efficient 1D gradient free optimization
Bracketing algorithms for minimizing one dimensional unimodal functions have the form:
- Suppose
is an interval containing the minimizer
;
- Pick
in
and evaluate the function at these points.
- If
then choose
- If
then choose
- Stop the process when
has a length smaller than a given tolerance or a given maximum number of function evaluations is reached.
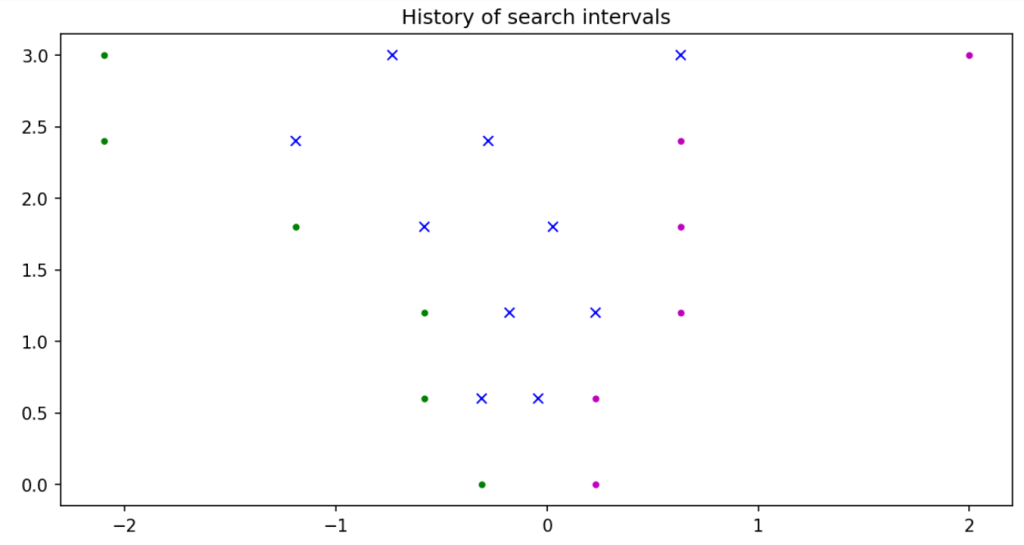
The simplest algorithm corresponds to choosing which divide the interval
into three equal parts. This algorithm can be called trisection algorithm. Below you can see the intervals and intermediary points
for a few iterations in the trisection algorithm.
Optimizing a 1D function – trisection algorithm
Optimization problems take the classical form
Not all such problems have explicit solution, therefore numerical algorithms may help approximate potential solutions.
Numerical algorithms generally produce a sequence which approximates the minimizer. Information regarding function values and its derivatives are used to generate such an approximation.
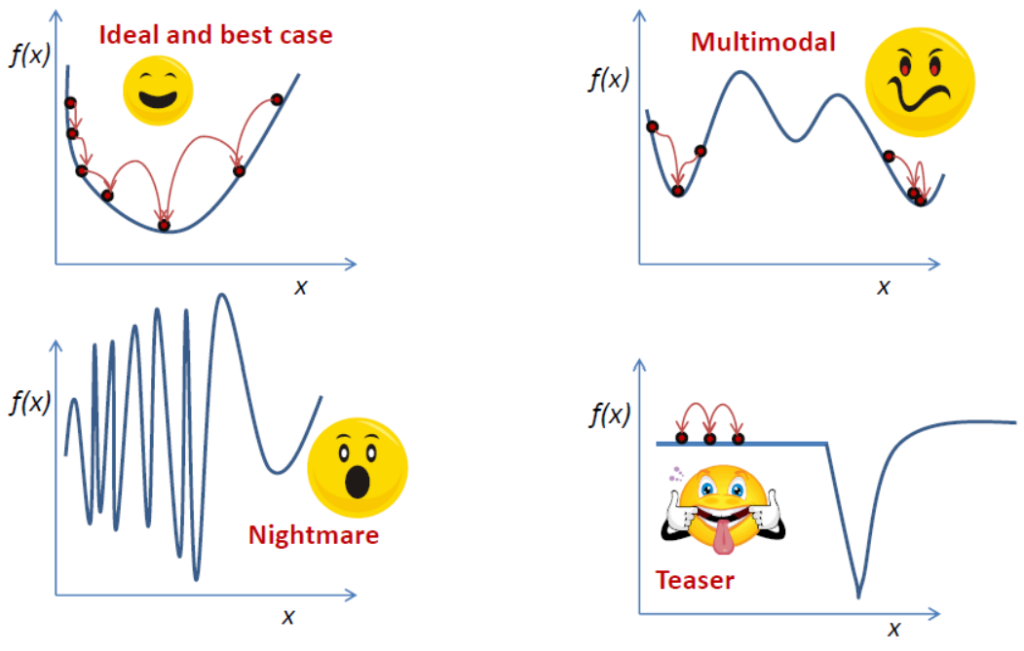
The easiest context is one dimensional optimization. The basic intuition regarding optimization algorithms starts by understanding the 1D case. Not all problems are easy to handle for a numerical optimization algorithm. Take a look at the picture below:
Read more…An inequality involving complex numbers
Consider and
complex numbers
. Show that
if and only if .
Proposed by Dan Stefan Marinescu in the Romanian Mathematical Gazette
Solution: For someone familiar with optimality conditions in multi-variable calculus this is straightforward. Notice that
is a convex function (linear combination of distances in the plane). The inequality is equivalent to , which means that
is the global minimum of the function.
For a convex, differentiable function global minimality is equivalent to verifying first order optimality conditions. Denoting ,
the partial derivatives of the function
with respect to
are
If then
and the conclusion follows. The converse also holds, obviously.
Since this problem was proposed for 10th grade, let’s use some simpler arguments to arrive to a proof. Denote by . A quick computation using properties of the modulus gives:
Thus . Of course, the classical inequality
implies
If the inequality in the statement of the problem holds, the above relation becomes an equality and for all
. Therefore points
belong to the mediatrix of the segment
. Therefore the centroid
also belongs to this mediatrix and to
, which implies
, as requested.
Conversely, if consider the inequality
to conclude.
Romanian Regional Olympiad 2024 – 10th grade
Problem 1. Let ,
,
. Find the smallest real number
such that
Problem 2. Consider a triangle inscribed in the circle
of center
and radius
. For any
denote by
where
are the orthocenters of the triangles
, respectively.
a) Prove that if the triangle is equilateral then
for every
.
b) Show that if there exist three distinct points such that
, then the triangle
is equilateral.
Problem 3. Let be three non-zero complex numbers with the same modulus for which
and
are real numbers. Show that for every positive integer
the number
is real.
Problem 4. Let . Determine all functions
which verify
for every and such that
has a unique solution.
Hints:
Problem 1: study the monotonicity of the function . Then observe that the inequality is equivalent to
.
Problem 2: Recall the identity whenever
is the orthocenter of
with circumcenter
. This can be proved using complex numbers and recalling that
, where
is the center of gravity. Therefore
and the analogue equalities. Summing we get
a) When
is equilateral and inscribed in a circle of radius
we have
. Moreover, the identity In particular, one can prove the following:
applied to the triangle equilateral triangle
with centroid
shows that
Thus
b) Assume there exist three distinct points such that
. This implies that
The relation above concerning the center of gravity of
shows that
. Since the points are distinct, it follows that
coincides with
, the circumcenter of
, therefore
is equilateral.
Problem 3: Denote the common value of the modulus:
. Then
Since
it follows that
. Then of course
. Finally, we know that
are roots of
Since the coefficients of this polynomial are real, an inductive argument shows that if
are real then
is real, finishing the proof.
Problem 4. Take and get
. Thus,
is the identity mapping on its image!! Take
and observe that
. Therefore
for any
. Since the equation
has a unique solution, it follows that
and
for
. Take
and get
. Therefore
for any
. Since
takes all positive values in
it follows that
for every
,
. Coupled with
this implies that
for all
. If
it follows that
therefore
. From
we obtain
for all reals
. It should be noted that this function obviously verifies the functional equation!
Putnam 2023 A1-A3
A1. For a positive integer , let
. Find the smallest
such that
.
Hints: Observe that
Differentiate again and observe that
It is straightforward now to evaluate and to answer the question.
A2. Let be an even positive integer. Let
be a monic, real polynomial of degree
; that is to say,
for some real coefficients
. Suppose that
for all integers
such that
. Find all other real numbers
for which
.
Hints: Denote . Then
is a polynomial of degree
. Moreover,
for
, showing that
has the
roots
.
It follows that . Identifying coefficients one finds
,
and the value of
is obtained by observing that the constant term in
should be zero. Then the answer to the question is obtained by investigating the roots of
. I guess a distinction should be made between the cases
even or odd, since it seems that the sign of
depends on that.
A3. Determine the smallest positive real number such that there exist differentiable functions
and
satisfying
- (a)
,
- (b)
,
- (c)
for all
,
- (d)
for all
, and
- (e)
.
Hints: Of course, an example of functions are
and
. This suggests that the answer could be
. In any case, this example shows that the smallest
verifies
.
Assuming that is the smallest zero, on
we have
. Now let’s try to obtain some differential inequality using the hypothesis:
where the last inequality follows from .
Therefore verifies
and
Therefore we have on
with
. The general solution is
The initial conditions show that . Therefore
and since we have
on
. Moreover
which is also non-negative on
. This implies
Thus the smallest such that
is indeed
.
Algebraic proof of the Finsler-Hadwiger inequality
Weitzenbock’s inequality states that if are the side lengths of a triangle with area
then
A strengthening of this result due to Finsler and Hadwiger states
A variety of proofs rely on various trigonometric or geometric arguments. Below you can find a purely algebraic argument based on the classical characterization: are side lengths of a triangle if and only if there exist
such that
,
,
. If
are strictly positive then the triangle will be non-degenerate.
Replacing with the above formulas replaces an inequality in a triangle with a general inequality where only positivity of the variables is involved. With this substitution, using classical notation for cyclic sums gives
and
On the other hand the area given by Heron’s formula is
Thus, Weitzenbock’s inequality is equivalent to
and the Finsler-Hadwiger inequality is equivalent to
This inequality follows at once, since squaring both sides gives
which is a well known consequence of
Equality holds, of course, if and only if . If the triangle is non-degenerate then it must be equilateral. Thus, Weitzenbock and Finsler-Hadwiger inequalities follow at once from classical inequalities, once the side lengths of a triangle are replaced with unconstrained variables.
A proof of the Hadwiger Finsler inequality
The Hadwiger-Finsler inequality states that if are the side lengths of a triangle with area
then
This was discussed previously on the blog. This post shows a translation of the original paper by Hadwiger and Finsler and this post shows a surprising geometrical proof.
Various proofs of the inequality are known. However, since an equality always beats an inequality, let us prove the identity
It is immediate to see that Jensen’s inequality applied to the tangent function, which is convex on is enough to deduce the Hadwiger-Finsler inequality from the above identity. To prove the identity, simply compute
Replacing the usual formula gives
Summing these identities for the three angles gives precisely the desired result. The same proof can be found, for example, here.
Is the Earth flat?
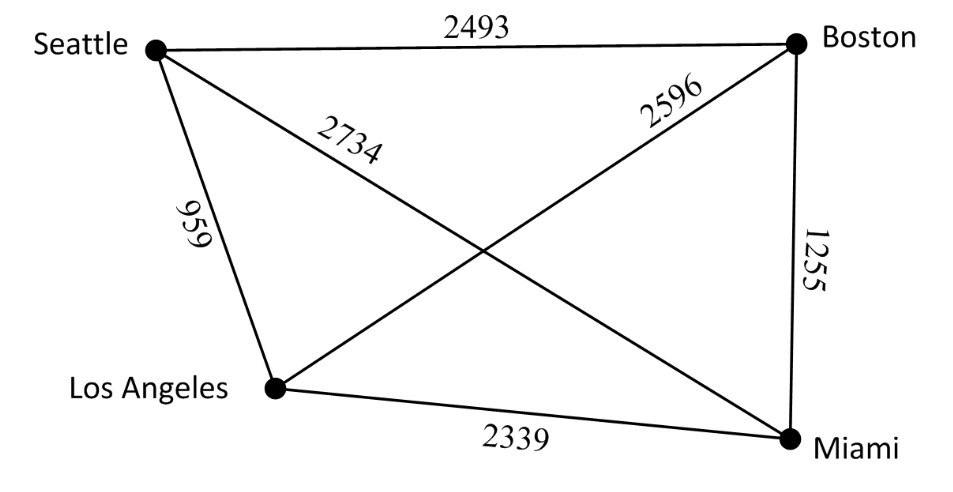
Consider the following experiment: the pairwise distances between four cities on Earth are given. Can you answer the following questions:
1) Can these distances be realized in a flat Earth?
2) Assuming the Earth is spherical and distances are measured along geodesics, can you determine the radius?
The test case was inspired from the following note. The initial test case involves the cities: Seattle, Boston, Los Angeles and Miami. A second test case is provided below.
You can use the Python code to create new test cases of your own.
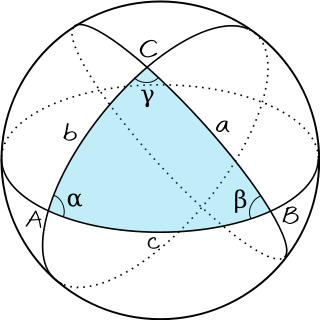
Read more…Area of a spherical triangle
A spherical triangle is obtained by joining three points ,
,
by geodesics. Assume the sphere has unit radius and the three points are contained in a half sphere. Then the area of the spherical triangle
is given by
where are the angles of the spherical triangle
.
Proof: Draw the great circles associated to ,
, meeting again at the point
, the diametrically opposite point to
. The resulting (double) slice
of the sphere has are
of the area of the sphere. Since the area of the sphere equals
, it follows that the slice has area
. The analogue slices
of the sphere associated to vertices
and
have areas
and
respectively. Let us observe that the slices
cover the whole sphere in the following way: the triangles
and
being covered three times and every other point is covered once. Therefore, the sum
equals the area of the sphere plus four times the area of the triangle
. The result follows dividing by four.
The image was taken from here.
Area of a spherical rectangle
A spherical rectangle is a spherical geodesic quadrilateral whose vertices form an Euclidean rectangle. In other words, the opposite edges are equal and all angles are equal. Suppose the side lengths
of pairs of opposite sides are known. Show that the area of the rectangle is given by
Maximal area polygons contained in disk/ellipse
Consider the unit disk and
. Prove that the
-gon of maximal area contained in
is the inscribed regular
-gon.
Deduce that the maximal area -gon inscribed in an ellipse is not unique.
This was inspired by the following MathOverflow question.
Solution: Obviously, a maximal area polygon will be convex, otherwise take the convex hull.
First, observe that an -gon contained in
is not maximal for the area if one of its vertices does not belong to
. Indeed, it is enough to pick a vertex
of
which does not belong to
and move it in the direction orthogonal to the adjacent diagonal towards
. This movement will increase the area.
Moreover, any maximal area polygon must contain the center of . If not, then such a polygon would be strictly contained in a half disk. A translation and a dilation could further increase the area, contradicting optimality. Thus, the maximal area
-gon is an inscribed
-gon.
Such a polygon is completely characterized (up to a permutation of its sides) by the lengths of its sides, or equivalently, the angles at the center of made by the sides. Consider
the angles at the center for an inscribed
-gon. Then its area is simply
Since and
is concave on
, Jensen’s inequality shows that the maximal area is attained for the regular
-gon.
Any ellipse is an image of the disk through an affine transformation. Since affine transformations preserve area ratios, any image of a in inscribed regular -gon in
through the affine mapping will produce an
-gon of maximal area contained in the ellipse. This provides an infinite family of non-equal
gons which maximize the area.
IMO 2023 Problem 2
Problem 2. Let be an acute-angled triangle with
. Let
be the circumcircle of
. Let
be the midpoint of the arc
of
containing
. The perpendicular from
to
meets
at
and meets
again at
. The line through
parallel to
meets line
at
. Denote the circumcircle of triangle
by
. Let
meet
again at
.
Prove that the line tangent to at
meets line
on the internal angle bisector of
.
Solution: Let us first do some angle chasing. Since we have
and since
is cyclic we have
. Therefore, if
we have
. Therefore the arcs
and
are equal.
Denote by the midpoint of the short arc
of
. Then
is the angle bisector of
. Moreover,
and
are symmetric with respect to
and
is a diameter in
.
Let us denote . It is straightforward to see that
, and since
we have
.
Moreover, . Considering
, since
we find that
is the midpoint of
. Then, since
in
we find that
is the midpoint of
. But
, since
is a diameter. It follows that
.
On the other hand, , showing that
is cyclic and
is tangent to the circle circumscribed to
. As shown in the figure below, the geometry of this problem is quite rich.
There are quite a few inscribed hexagon where Pascal’s theorem could be applied. Moreover, to reach the conclusion of the problem it would be enough to prove that and
are concurrent, where
is the symmetric of
with respect to
.

IMO 2023 Problem 4
Problem 4. Let be pairwise different positive real numbers such that
is an integer for every
Prove that
IMO 2023 Problem 1
Problem 1. Determine all composite integers that satisfy the following property: if
are all the positive divisors of
with
, then
divides
for every
.
Problems of the International Mathematical Olympiad 2023
Problem 1. Determine all composite integers that satisfy the following property: if
are all the positive divisors of
with
, then
divides
for every
.
Problem 2. Let be an acute-angled triangle with
. Let
be the circumcircle of
. Let
be the midpoint of the arc
of
containing
. The perpendicular from
to
meets
at
and meets
again at
. The line through
parallel to
meets line
at
. Denote the circumcircle of triangle
by
. Let
meet
again at
. Prove that the line tangent to
at
meets line
on the internal angle bisector of
.
Problem 3. For each integer , determine all infinite sequences of positive integers
for which there exists a polynomial
of the form
, where
are non-negative integers, such that
for every integer .
Problem 4. Let be pairwise different positive real numbers such that
is an integer for every Prove that
Problem 5. Let be a positive integer. A Japanese triangle consists of
circles arranged in an equilateral triangular shape such that for each
,
,
,
, the
row contains exactly
circles, exactly one of which is coloured red. A ninja path in a Japanese triangle is a sequence of
circles obtained by starting in the top row, then repeatedly going from a circle to one of the two circles immediately below it and finishing in the bottom row. Here is an example of a Japanese triangle with
, along with a ninja path in that triangle containing two red circles.

In terms of , find the greatest
such that in each Japanese triangle there is a ninja path containing at least
red circles.
Problem 6. Let be an equilateral triangle. Let
be interior points of
such that
,
,
, and
Let and
meet at
let
and
meet at
and let
and
meet at
Prove that if triangle
is scalene, then the three circumcircles of triangles
and
all pass through two common points.
(Note: a scalene triangle is one where no two sides have equal length.)
Source: imo-official.org, AOPS forums
Polygon with an odd number of sides
Let be a convex polygon. Suppose there exists a point
inside the polygon such that each one of the segments
,
intersects exactly one side of the polygon in its interior. Prove that
is odd.
Alternative reformulation: Let be a convex polygon with an even number of sides and
be an interior point. Then there exist two of the segments
which intersect the same side.
Romanian Team Selection test 2007
Read more…A series involving a multiplicative function
Let be a function with the property that
for any
. Moreover, suppose that
for all
, where
is the
-th prime number.
Prove that
I posted this problem quite a while back. Here is a solution I found recently.
Read more…Maximize the circumradius of a unit diameter simplex
Given a simplex in dimension with diameter at most equal to one, what is its largest possible circumradius? The question is well posed, since a ball of diameter
will cover all the points (a ball of radius
centered at one of the given points).
Consider points in dimension
and suppose the origin is the center of the circumscribed ball. Then given two vertices
, the circumradius verifies
. Therefore, one should maximize the minimal cosine of angles of two such vectors.
An immediate upper bound, which is tight can be obtained from the identity . It can be seen that
. Thus the maximal circumradius verifies
This coincides with the case where all angles between different vectors are equal and their cosine is
, i.e. the simplex is regular.